- Objects: A, B, people, numbers, colors, wars, theories, squares, pits, wumpus, .
- Relations:It can be unary relation such as: red, round, is adjacent, or n-any relation such as: the sister of, brother of, has color, comes between
- Function: Father of, best friend, third inning of, end of, .
- Syntax
- Semantics
Syntax of First-Order logic:
The syntax of FOL determines which collection of symbols is a logical expression in first-order logic. The basic syntactic elements of first-order logic are symbols. We write statements in short-hand notation in FOL.
Basic Elements of First-order logic:
Following are the basic elements of FOL syntax:
| Constant | 1, 2, A, John, Mumbai, cat. |
| Variables | x, y, z, a, b. |
| Predicates | Brother, Father, >. |
| Function | sqrt, LeftLegOf, . |
| Connectives | ∧, ∨, ¬, ⇒, ⇔ |
| Equality | == |
| Quantifier | ∀, ∃ |
Atomic sentences:
- Atomic sentences are the most basic sentences of first-order logic. These sentences are formed from a predicate symbol followed by a parenthesis with a sequence of terms.
- We can represent atomic sentences as Predicate (term1, term2, . term n).
Example: Ravi and Ajay are brothers: => Brothers(Ravi, Ajay).
Chinky is a cat: => cat (Chinky).
Complex Sentences:
- Complex sentences are made by combining atomic sentences using connectives.
First-order logic statements can be divided into two parts:
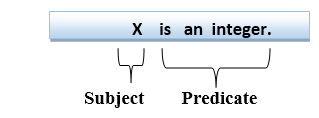
- Subject: Subject is the main part of the statement.
- Predicate: A predicate can be defined as a relation, which binds two atoms together in a statement.
Consider the statement: "x is an integer.", it consists of two parts, the first part x is the subject of the statement and second part "is an integer," is known as a predicate.
Quantifiers in First-order logic:
- A quantifier is a language element which generates quantification, and quantification specifies the quantity of specimen in the universe of discourse.
- These are the symbols that permit to determine or identify the range and scope of the variable in the logical expression. There are two types of quantifier:
- Universal Quantifier, (for all, everyone, everything)
- Existential quantifier, (for some, at least one).
Universal Quantifier:
Universal quantifier is a symbol of logical representation, which specifies that the statement within its range is true for everything or every instance of a particular thing.
The Universal quantifier is represented by a symbol ∀, which resembles an inverted A.
Note: In universal quantifier we use implication "→".
If x is a variable, then ∀x is read as:
Example:
All man drink coffee.
Let a variable x which refers to a cat so all x can be represented in UOD as below:
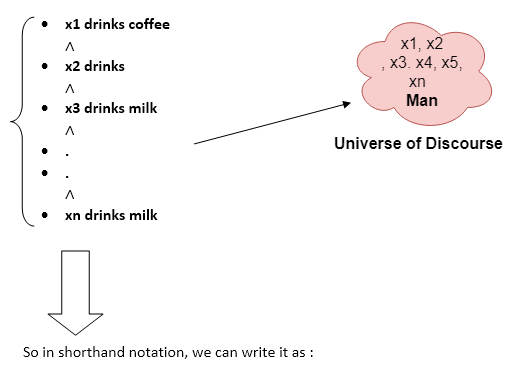
∀x man(x) → drink (x, coffee).
It will be read as: There are all x where x is a man who drink coffee.
Existential Quantifier:
Existential quantifiers are the type of quantifiers, which express that the statement within its scope is true for at least one instance of something.
It is denoted by the logical operator ∃, which resembles as inverted E. When it is used with a predicate variable then it is called as an existential quantifier.
Note: In Existential quantifier we always use AND or Conjunction symbol (∧).
If x is a variable, then existential quantifier will be ∃x or ∃(x). And it will be read as:
Example:
Some boys are intelligent.
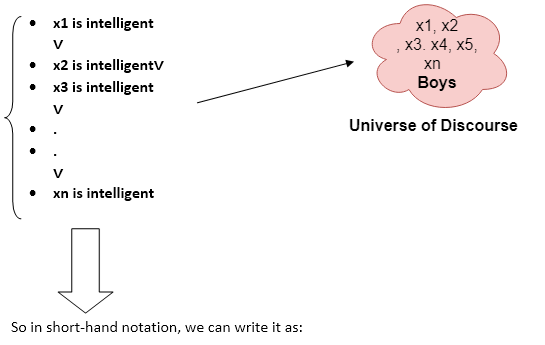
∃x: boys(x) ∧ intelligent(x)
It will be read as: There are some x where x is a boy who is intelligent.
Points to remember:
- The main connective for universal quantifier ∀ is implication →.
- The main connective for existential quantifier ∃ is and ∧.
Properties of Quantifiers:
- In universal quantifier, ∀x∀y is similar to ∀y∀x.
- In Existential quantifier, ∃x∃y is similar to ∃y∃x.
- ∃x∀y is not similar to ∀y∃x.
Some Examples of FOL using quantifier:
1. All birds fly.
In this question the predicate is "fly(bird)."
And since there are all birds who fly so it will be represented as follows.
∀x bird(x) →fly(x).
2. Every man respects his parent.
In this question, the predicate is "respect(x, y)," where x=man, and y= parent.
Since there is every man so will use ∀, and it will be represented as follows:
∀x man(x) → respects (x, parent).
3. Some boys play cricket.
In this question, the predicate is "play(x, y)," where x= boys, and y= game. Since there are some boys so we will use ∃, and it will be represented as:
∃x boys(x) → play(x, cricket).
4. Not all students like both Mathematics and Science.
In this question, the predicate is "like(x, y)," where x= student, and y= subject.
Since there are not all students, so we will use ∀ with negation, so following representation for this:
¬∀ (x) [ student(x) → like(x, Mathematics) ∧ like(x, Science)].
5. Only one student failed in Mathematics.
In this question, the predicate is "failed(x, y)," where x= student, and y= subject.
Since there is only one student who failed in Mathematics, so we will use following representation for this:
∃(x) [ student(x) → failed (x, Mathematics) ∧∀ (y) [¬(x==y) ∧ student(y) → ¬failed (x, Mathematics)].
Free and Bound Variables:
The quantifiers interact with variables which appear in a suitable way. There are two types of variables in First-order logic which are given below:
Free Variable: A variable is said to be a free variable in a formula if it occurs outside the scope of the quantifier.
Example: ∀x ∃(y)[P (x, y, z)], where z is a free variable.
Bound Variable: A variable is said to be a bound variable in a formula if it occurs within the scope of the quantifier.
Example: ∀x [A (x) B( y)], here x and y are the bound variables.